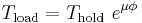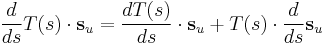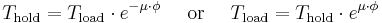Capstan equation
The capstan equation or belt friction equation, also known as Eytelwein's formula[1][2], relates the hold-force to the load-force if a flexible line is wound around a cylinder (a bollard, a winch or a capstan)[3] [4]. Because of the interaction of frictional forces and tension, the tension on a line wrapped around a capstan may be different on either side of the capstan. A small holding force exerted on one side can carry a much larger loading force on the other side; this is the principle by which a capstan-type device operates. For instance in rock climbing with so-called top-roping, a lighter person can hold (belay) a heavier person due to this effect.
The formula is:
where 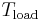 is the applied tension on the line,
is the applied tension on the line, 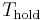 is the resulting force exerted at the other side of the capstan,
is the resulting force exerted at the other side of the capstan,  is the coefficient of friction between the rope and capstan materials, and
is the coefficient of friction between the rope and capstan materials, and  is the total angle swept by all turns of the rope, measured in radians (i.e., with one full turn the angle
is the total angle swept by all turns of the rope, measured in radians (i.e., with one full turn the angle 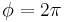 ).
).
Several assumptions must be true for the formula to be valid:
- The rope is on the verge of full sliding, i.e.
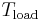 is the maximum load that one can hold. Smaller loads can be held as well, resulting in a smaller effective contact angle
is the maximum load that one can hold. Smaller loads can be held as well, resulting in a smaller effective contact angle  .
. - It is important that the line is not rigid, in which case significant force would be lost in the bending of the line tightly around the cylinder. (The equation must be modified for this case.) For instance a Bowden cable is to some extent rigid and doesn't obey the principles of the Capstan equation.
- The line is non-elastic.
It can be observed that the force gain grows exponentially with the coefficient of friction, the number of turns around the cylinder, and the angle of contact. Note that the radius of the cylinder has no influence on the force gain. In the table below are listed 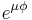 for different numbers of turns and different values of
for different numbers of turns and different values of 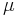
(No. turns vertical, coefficient of friction  horizontal)
horizontal)
From the table it is evident why one seldom sees a sheet (a sailing rope) wound more than three turns around a winch. The force gain would be extreme and would be counter-productive since there is risk for a riding turn, meaning that the sheet will not run out when one lets go of the hold end. A modern winch is not exactly circular if seen from above, it usually has what can be best described as "inverted fluting", this is to increase the friction, but only for tangential slip, the rope coils can still slip unobstructed axially avoiding riding turns.
For instance, the factor 153552935 means, in theory, that a newborn baby would be capable of holding the weight of two "USS Nimitz" supercarriers (97 000 ton each, but for the baby it would be only a little more than 1 kg).
Proof of the capstan equation
1. Circular coordinates
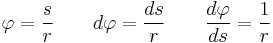 (1), (2), (3)
(1), (2), (3)
Let  and
and 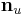 denote unit vectors;
denote unit vectors;
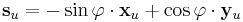 (4)
(4)
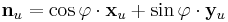 (5)
(5)
Then from (5)
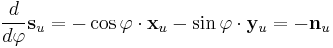 (6)
(6)
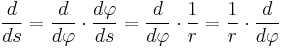 (7)
(7)
From (6) and (7), it follows that
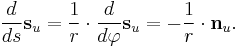 (8)
(8)
2. Forces on cordage in general
Now, let's study a piece of cord in general, subject to an arbitrary force. Let 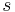 denote the length of the cord and let the force per unit length be
denote the length of the cord and let the force per unit length be 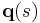 . Consider a short piece
. Consider a short piece 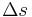 of the cord and introduce the cross-sectional force
of the cord and introduce the cross-sectional force 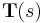 . Balancing the forces, we get
. Balancing the forces, we get
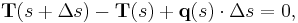 (9)
(9)
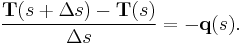 (10)
(10)
Letting 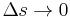 , we conclude that
, we conclude that
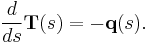 (11)
(11)
3. A line around a capstan
A line is wound around a cylinder(a bollard or a capstan). In this case the curvature of the line is circular which makes the problem easier. Let 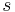 be the length of the line from a point A where the line makes contact with the cylinder. At the point
be the length of the line from a point A where the line makes contact with the cylinder. At the point 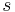 on the short piece
on the short piece 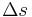 of the line acts a force from the cylinder that can be subdivided into a tangential component
of the line acts a force from the cylinder that can be subdivided into a tangential component  (friction) and a normal component
(friction) and a normal component  . That is to say that
. That is to say that
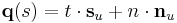 (12)
(12)
With the cross-sectional force 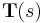 (which is tangential) we get
(which is tangential) we get
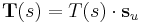 (13)
(13)
From (11), (12) and (13), it follows that
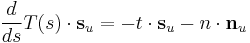 (14)
(14)
Derivative of a product and (8) imply that
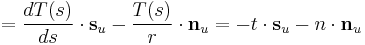 (15)
(15)
Identifying components in (15), we get
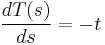 (16)
(16)
and
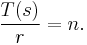 (17)
(17)
Dividing (16) by (17), we get
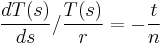 (18)
(18)
From (18) and reciprocal of (2), we get
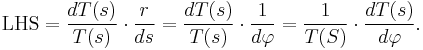 (19)
(19)
From (18) and (19) it follows that
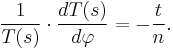 (20)
(20)
Let 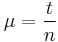 (21) be the coefficient of friction (no slip). Then
(21) be the coefficient of friction (no slip). Then
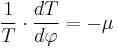 (22) :
(22) : 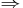
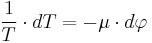 (23)
(23)
Integration of (23) yields
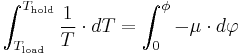 (24)
(24)
 (25)
(25) 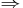
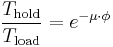 (26)
(26)
Finally,
See also
References
- ^ http://www.esr.ruhr-uni-bochum.de/rt1/currentcourse/node57.html
- ^ http://www.jrre.org/att_frict.pdf
- ^ Johnson, K.L. (1985) (PDF). Contact Mechanics. http://www.knovel.com/web/portal/browse/display?_EXT_KNOVEL_DISPLAY_bookid=2685. Retrieved February 14, 2011.
- ^ Attaway, Stephen W. (1999). "The Mechanics of Friction in Rope Rescue" (PDF). International Technical Rescue Symposium. http://www.jrre.org/att_frict.pdf. Retrieved February 1, 2010.
- Arne Kihlberg, Kompendium i Mekanik för E1, del II, Göteborg 1980, 60–62